Constant Time Stateless Shuffling and Grouping

By Alan Wolfe & William Donnelly – Electronic Arts SEED Future Graphics Team
Game development combines hard work and obscure tidbits of math and computer science to make the seemingly impossible happen in real time. In this article, we will talk about shuffling items and arranging them into groups of specific sizes — without actually shuffling or grouping anything.
The code that goes along with this post can be found at https://github.com/SEED-EA/O1ShufflingGrouping

Stateless Shuffling
Shuffling an array randomly reorders the items in that array.
In other words, shuffling changes the index of an array item within that array.
Because shuffling an array doesn't create or delete items, we know that (1) each index before shuffling maps to exactly one index after shuffling, and (2) each index after shuffling maps to exactly one index before shuffling. Even if an array item is randomly shuffled into the same position it was in initially (which would result in it having the same index before and after shuffling), it is still a one-to-one mapping.
Mathematics has a special name for this kind of one-to-one mapping — a Bijection —and in computer science, any reversible operation is bijective. This means that we can make a bijection by pairing addition with subtraction, or by pairing XOR with itself, but we cannot use things like integer division or bit shifting, as those can cause us to lose information.
Computer science often uses hashes in algorithms, but hashes are designed to be one-directional. Hashes also allow collisions in their output, making it impossible to reverse a hashing algorithm unambiguously. But while hashes are not reversible, encryption is. If you encrypt data with a key, you can unencrypt the result (the cipher text) with the same key to recover the original data (the plain text).That means that we can use encryption to make a bijection, which in turn enables us to make a mapping from a starting array index to a shuffled index.
Shuffling with Encryption Keys
With this method of mapping we’re able to say: “We are at index 2 in the array. What index is this item at after shuffling?”. Let’s assume we encrypt 2 and get an answer of 48. We can then ask the reverse question: “Where was index 48 before the shuffle?”. Decrypting 48 gives us our answer of 2. The key we used to encrypt /decrypt our number can also be used as a random seed for the shuffle, allowing for an arbitrary number of different shuffles. Contrast this with a Gray code (https://en.wikipedia.org/wiki/Gray_code) — which isn’t seedable and offers only one shuffle order — and you quickly begin to see the advantage.
Shuffling isn’t the only advantage of using this mapping method: it also allows you to generate pseudo-random numbers without repetition. For instance, let’s say you want to generate all numbers between 0 and 65,535 in a random order, making sure not to repeat any. You would start by looping from 0 to 65535 and — inside the loop — encrypt the index with a 16-bit block cipher to get the following random number.With this method there can’t be any repeats because a repeat wouldn’t be decryptable (and so wouldn’t be encryption). This technique is called “Format-preserving encryption” (https://en.wikipedia.org/wiki/Format-preserving_encryption) and is rumored to be how credit card companies generate new credit card numbers that (1) don’t use a number that was previously issued and (2) are cryptographically randomized so that their numbers can’t be guessed. Without this method, credit card companies would need to generate a random card number, scan every credit card issued to avoid duplicating an earlier number, and continue this time-consuming loop until they found an unused number!
In practice, encryption algorithms for massive financial systems are extremely slow and don’t run in real time. Luckily for us, a shuffle designed for graphics or game development purposes doesn't need cryptographic strength algorithms, so we can relax the quality and make something usable for our needs.
Feistel Networks
Ultimately, you want a symmetric key N-bit block cipher where 2^N is the size of the data you want to shuffle. You also want it to be fast enough to run in real time.
There are a few ways to craft your own block cipher, but we recommend using Feistel networks (https://en.wikipedia.org/wiki/Feistel_cipher). They break the data in half, run one half through a “round” function to get a value to XOR the other half by, swap the halves, and then put it back together for the next round. The round function can use anything, including destructive operations, so a nice fast hash like PCG (https://www.pcg-random.org) is a good choice here.or more information on fast hashes, check here (https://jcgt.org/published/0009/03/02/) and here (https://www.reedbeta.com/blog/hash-functions-for-gpu-rendering/).
The number of rounds in a Feistel network is also tuneable for quality versus speed. More iterations means higher quality, but also more execution time.
You can also use this method to shuffle a non-2^N number of items, but it gets a little more complicated. Let’s call the number of items k and the next power of two N. You iterate through the shuffle from 0 to N, encrypting the index to get the shuffled index, but ignore anything larger than or equal to k in the output. In this sense, if you had a shuffle iterator with a Next() operation, it internally would need to have a loop now because it has to skip an unknown number of items before getting the next valid item. This also makes asking, “where was this index before the shuffle” a bit more complicated because the location it gives you back is padded with any invalid / ignored indices that came before it.
A further complication comes up if you’re using a Feistel network to make your cipher, because the Feistel network algorithm wants to break your data in half. That means you want to have an EVEN number of bits in your cipher. (Unbalanced Feistel networks do exist, but the simplest implementation uses an even number of bits.)
This technique can still be useful with non powers of two, but it’s worth being aware of the issues.
Shuffling is Pairing
Format-preserving encryption isn’t just a great way to shuffle items — it can also be used to pair items together. Think of the index before shuffling as one of the items in a pair and the index after shuffling as the other item in a pair.
There are a couple of shortcomings, however. The first is that an item can sometimes be paired with itself (a fixed point), similar to how an item can be randomly shuffled into the same index it started with.. This isn’t a problem for many applications though, and having the odd “degenerate pair” is okay.
The second shortcoming of this method is that each item will appear in two pairs if it doesn’t pair with itself. This is because each index appears twice: once as the first item and once as the second item.
An easy way to overcome both of these issues is to break your items in half, making the first item index into the first half and the second item index into the second half. Your indices would then be 0 to N/2 instead of 0 to N. You can do this very simply by breaking your items into two lists: 0 to N/2-1 and N/2 to N.
Increasing Randomness
Keep in mind that when you limit the possibilities of which items can pair together, you are biasing the results — the more randomly you can classify items as A or B, the better your result will be. When we talk about increasing randomness, it’s in an “Avalanche Effect” sense, where a small change in the input causes a large change in the output. You must also be careful to ensure that your classifier classifies items evenly into both groups. Ultimately, you need this to be a bijection too, and the more it scrambles the input to the output, the better. Using low-grade encryption to see if the result is odd or even could be a good choice here. The more random your classification is, the less biased it will be. If you are doing many shuffles or pairings over time, changing the classification for each shuffle is another great way to reduce bias. If you’re using encryption mod 2 for your classification, you can achieve this by changing the encryption key each time:

A Pixel Pair Problem
Let’s say you are in a compute shader doing work for a specific pixel and want to coordinate with another randomly-paired pixel. Maybe these two pixels are going to do some logic to see if they should swap places.
So, you know you are at pixel A, and you reach for your bijection code to find the index of pixel B, and then it hits you… do you encrypt or decrypt to get the other pixel you are working with? Is this pixel the first item, or is the other pixel the first item?
If you broke the list into two parts, as discussed in the last section, you could use that information to figure out which pixel was first — but what if you didn’t do that?
In this case, a bijection isn’t enough: We need an involution. An involution is a bijection that is its own inverse. That means that instead of having both an encrypt and decrypt function, we have a single “Xcrypt” function that you call once to encrypt something and again to decrypt it. An example of an involution you are likely familiar with is XORing against a constant. If you XOR a number by a constant twice in a row, you get the original number back.
With an involution, you don’t need to know if you’re looking at the first or second item. If you call your Xcrypt function, you’ll get the other item in your pair. And if you do need an order for some reason, you can always say that the lower-valued index is the first item. For a 2D pixel coordinate, you can multiply y by imageWidth and add x to get a 1d value for this ordering comparison.
How do you make arbitrary involutions? There’s a neat trick for turning a bijection into an involution: (1) encrypt your index, (2) apply an involution (such as XORing against a constant), and then (3) decrypt your index.
Grouping
So: You know how to shuffle and pair objects. But how do you group them into larger groups? The answer is a pretty straightforward extension to pairing.
A basic involution is a function that, when called twice, returns you to your original value. But there are higher-order involutions that take other numbers of repeated calls to return to the original value. Multiplying by “Roots of unity” (https://en.wikipedia.org/wiki/Root_of_unity) can make functions with arbitrary cycle lengths, but they work with complex numbers. A much simpler method that will work for us is using modulus! An order N involution can be defined as below in integer math:
F(x) = N*(x/N)+((x+1)%N
Let’s show an example with N being 3. If x is 4, it outputs 5. If x is 5, it outputs 3. If x is 3, it outputs 4 — and the cycle is finished repeating.
Much like the shuffling example and working with non powers of two, if your items are not evenly divisible by N, the grouping will contain some invalid indices beyond the number of items you have. If you were grouping 8 items into groups of 3 for instance, some of the groups would contain the number 9, which is invalid.
If this was a problem and you absolutely needed it to never give you invalid indices, you could group all the invalid indices into a single cycle or make them fixed points. In both cases, they would only ever choose themselves, so no valid item would ever find itself grouped with invalid items. How do you do that? Well, you have “infinite” time at preprocessing time to do the right thing at run time, so you could just search (algorithmically) for a combination of bijections and involutions to give you this property. This is very similar to the type of thing we do to find “minimal perfect hashes” (https://en.wikipedia.org/wiki/Perfect_hash_function). You could use this same technique to making sure there were no fixed points in your shuffling.
Now we’re ready to go create a framework in which we can shuffle, inverse shuffle, and group items together — all in a stateless and real-time-friendly way.
Demonstrations
The code that goes along with this article (at https://github.com/SEED-EA/O1ShufflingGrouping) implements two objects: a StatelessShuffle object, and a StatelessGrouping object. These objects are use in four demonstrations in the code, and explained below.
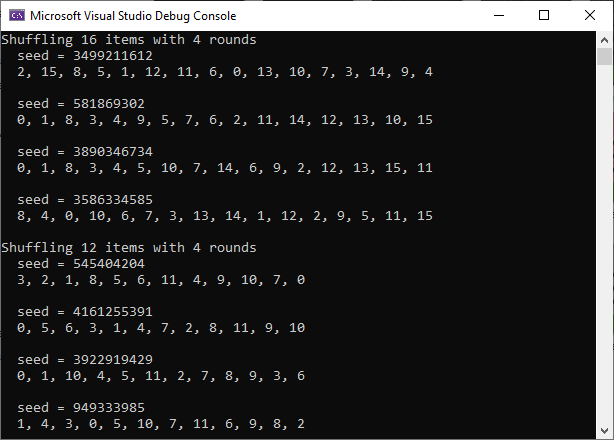
The first demonstration is ShuffleTest(), which shows you how to use a StatelessShuffle object to sort a list of 16 items with different seeds. It also shows you how to sort a list of objects with 12 items, which is not a power of two.
The second demonstration is FadeInTest() which uses a StatelessShuffle object to set pixels in a random order and make an image emerge over time. It uses the frame index to find the next pixel to set from a source image. All pixels are visited exactly once, gradually filling in the image until it’s complete.

The third demonstration is FadeInRGBTest(), which uses a StatelessGrouping object to group pixels into groups of three. It uses the frame number of each frame to get a group of three pixels, and sets the R, G, and B channels of each of those pixels, respectively. Since the group membership order is relative to the group member asking, and each group member gets visited by the loop, each pixel will set each channel by the end. In this setup, the group's first member is the unaltered index of the item asking for the group members, which is the frame numbers, so you can see the red channel filling from top to bottom while the green and blue channels fill randomly.

To fix this, we could use a StatelessShuffle object to randomize the order of the groups and thus randomize the red channel, but instead, we make the StatelessGrouping object group pixels into groups of four. We use the last three members as the pixels to set the red, green, and blue channels for, each pixel, which gives us a randomized ordering for all pixels and all channels. This fourth demonstration is FadeInRGB2Test().


