By Alan Wolfe – Electronic Arts SEED Future Graphics Team

Machine learning (ML) is a powerful tool that’s already in use across game development, supporting everything from asset creation to automated testing. As an accelerant, it allows developers to create better-looking, higher-quality games with less time and effort, and in the future, it could even enable game teams to create things that are currently impossible due to time, cost, and effort constraints.

However, one challenge of applying machine learning to game development is the significant difference between the two disciplines. It’s rare for a machine learning practitioner to understand the ins and outs of game development, or for a game developer to understand the complexities of machine learning. And while this has begun to change more recently, we still have a long way to go.

With this article, we hope to help bridge the knowledge gap between ML and game dev with a developer-friendly introduction to machine learning. We’ll be breaking this into three parts with accompanying exercises so you can practice what you learn:

1. Multilayer perceptrons — Understanding and working with a “classic” neural network.
2. Gradients — An introduction to gradient descent and three ways to calculate gradients.
3. Hands-on training — Using C++ to train a neural network to recognize hand-drawn digits.

Multilayer Perceptrons

Multilayer perceptrons (MLPs) are “classic” neural networks made up of multiple layers of individual neurons. In an MLP, each neuron in a layer connects to all neurons in the previous and subsequent layers, creating a fully connected network.

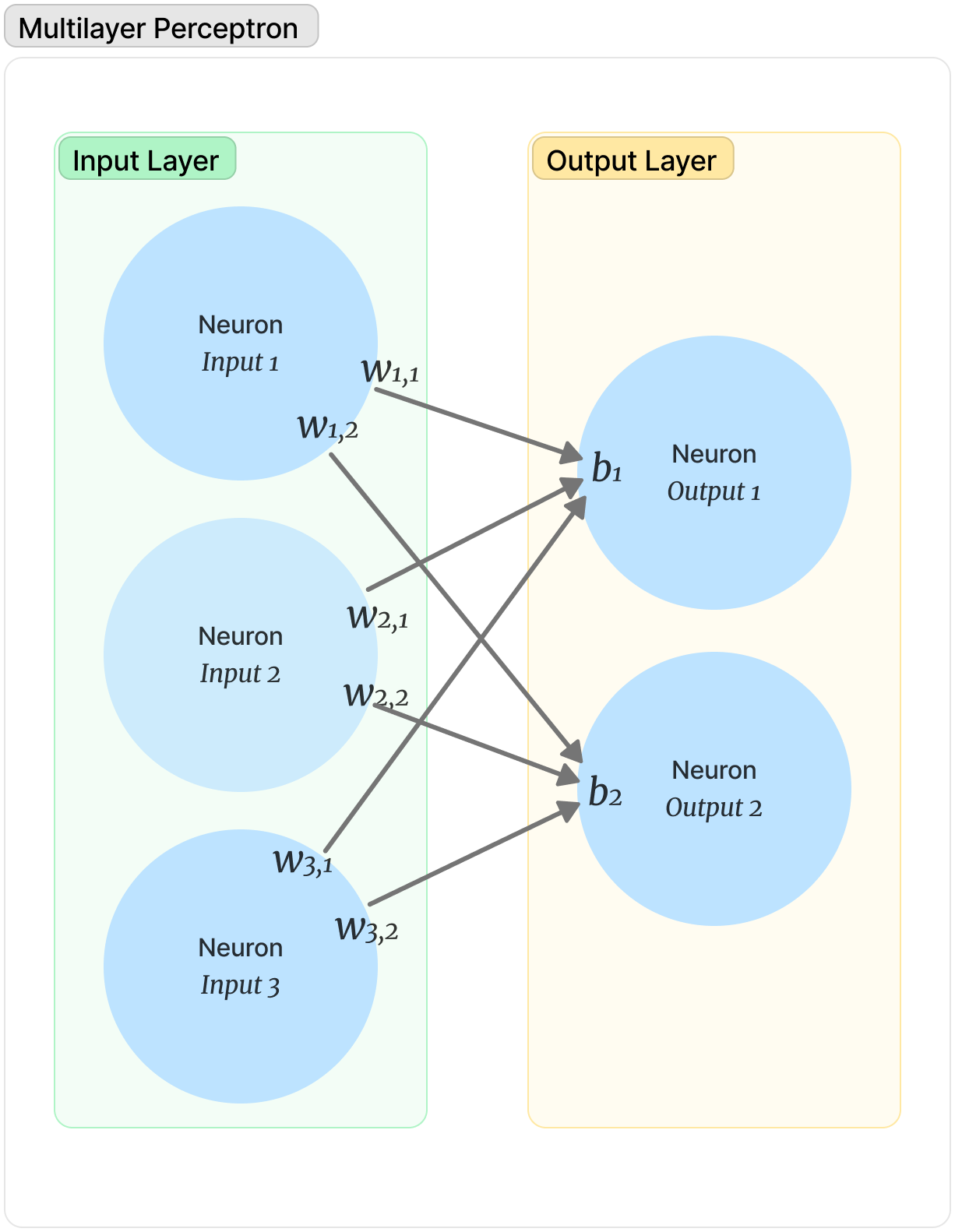
A multilayer perceptron with an input layer, an output layer, and no hidden layers. Each neuron in the input layer is connected to all neurons in the output layer.

Each connection between two neurons has a weight (w_x,y) that determines the strength of that connection. Each neuron also has a bias (b_x) — an additional input that can influence the overall strength of a connection. Weights and biases are the levers we use during training to change the way that our inputs map to outputs.

When evaluating a network, we arrive at the value of a specific neuron by calculating the sum of (Input_x * w + b) for each connection leading into that node. So if we wanted to get the value of the Output 1 neuron in the diagram above, we would use:

(Input₁ * w_1,1 ) + (Input₂ * w_2,1) + (Input₃ * w_3,1) + b₁

That sum is then put through a nonlinear activation function. One of the simplest activation functions is ReLU (rectified linear unit), which is just max(0,value). In our experiment, we’re going to use a simplified sign function that will return 1 if the value is greater than zero, and 0 if the value is equal to or less than zero.

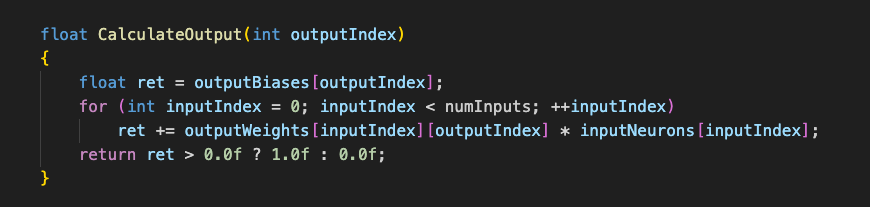
Explicitly evaluating a neuron. The trinary operation on the last line is the nonlinear activation sign function we described above.

Neuron Values as Dot Products

Another way to look at the calculation above is as a dot product of (1) the previous layer’s neuron values, and (2) the weights of the connections to the node you are calculating the value for. You could then choose to add the bias to the result, or you could include it in the dot product by making a fake neuron in the previous layer with a value of 1 and using the bias as the weight value.

Evaluating a neuron as a dot product. An extra neuron was added with a value of 1, and a connection weight of the bias to handle the bias term.

Since you have to find this dot product for each neuron in the current layer, you might as well use a matrix multiplication to calculate all N dot products at once. You can then apply the nonlinear activation function to each item in the resulting vector. That vector is now ready to go into the next matrix multiply to evaluate the next layer in the network.

Evaluating an entire layer as a matrix multiply. inputNeurons is a vector of the input layer neuron values. outputWeights is a matrix of biases and weights for all connections from the input layer to the output layer. inputNeurons contains an extra neuron with a value of 1, and outputWeights contains the neuron biases as connection weights with that neuron, to handle the bias terms.

Once you’ve seen how matrix multiplies can be used to evaluate neural network layers, you really start to understand why neural networks love running on GPUs. Sometimes when you spend decades working to maximize the number of vertices you can push through matrix multiplies to convert world space triangles to clip space triangles, you end up with hardware that’s great for graphics and machine learning!

Inputs and Outputs

MLPs take a floating point vector as input, but give an integer as output, which makes them binary classifiers. A common way to turn a network’s output into an integer is to take the index of the largest output neuron as the output of the network — a winner-take-all strategy. But when training an MLP, we give it both an input and an expected output, which makes it supervised learning.  An example of unsupervised learning would be finding the best way to group 1,000 objects into 3 groups, then leaving it up to the algorithm to define the groups. 

Going through an entire set of training data once is called an epoch. Updating weights and biases during an epoch instead of waiting until the end is called mini-batching. A multiplier for how much you update the weights during training is called the learning rate.

It’s also worth noting that while we use the term neuron when talking about neural networks, there are significant differences between neurons in machine learning neurons and neurons in human biology.

Exercise Set 1: Perceptron Logic Gates

Time for the first set of exercises!

The goal of this exercise is to see if you can manually figure out the weight and bias values to give to these small neural networks to calculate OR, AND, NOT, and XOR. Detailed instructions and solutions can be found at https://github.com/electronicarts/cpp-ml-intro/tree/main/Exercises/1_LogicGates.